TreeviewCopyright © aleen42 all right reserved, powered by aleen42
Longest Common Sub-sequence Problem(最長公共子序列) Back
Overview
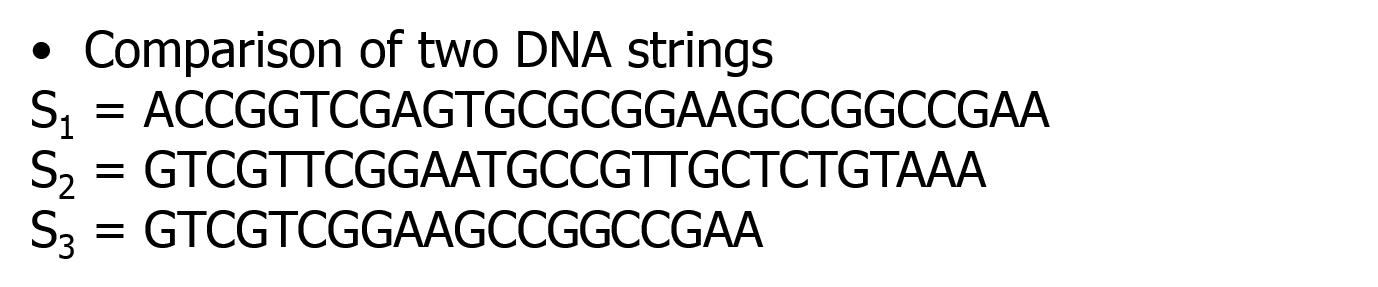
- 求出最短裝配時間
- 主程序的時間複雜度:
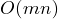
- 追溯最優解的時間複雜度:
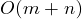
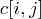: S1序列取前i個, S2序列取前j個時的最長公共子序列長度值. (用於求最優解的值)
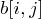: S1序列取前i個, S2序列取前j個時, 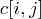是如何求得. (用於求最優解)
Optimal Substructure
- 當我們知道若求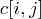的時候, 若S1序列的最後一個字符與S2的最後一個字符相同, 則該字符一定在公共子序列中, 因此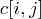的值必定是
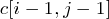的值加一; 否則, 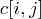的值將是
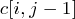和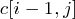
中較大的一個.
Recursive Expression
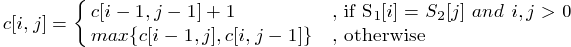
Solution
- 最優解: 通過反向遍曆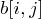, 找到最優解.
- 最優解的值:
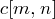
As the plugin is integrated with a code management system like GitLab or GitHub, you may have to auth with your account before leaving comments around this article.
Notice: This plugin has used Cookie to store your token with an expiration.