Binary Trees and Binary Search Trees Back
Sometimes, data will have a hierarchy, such as files in a file system, and for this kind of data, we will import trees to store them.
Trees Defined
A tree is made up of a set of nodes connected by edges. An example of a tree is a company's organizational chart (Figure 1), in which each box is a node, and the lines between two boxes are called edges.
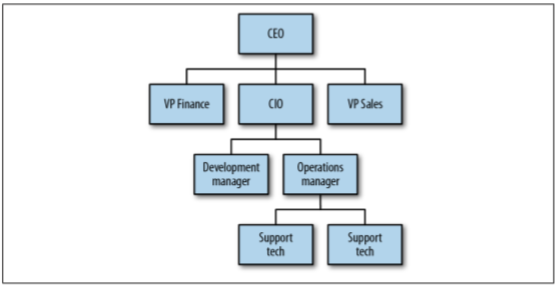
Figure 1 An organizational chart is a tree structure
The top node of a tree is called the root node. If a node is connected t other nodes below it, the preceding node is called the parent node, while the following one is called the child node. A ndoe without any child nodes is called a leaf node.
There is a special type of trees, called binary trees, restricting the number of child nodes to no more than two.
Visiting all nodes in a tree in some particular order is know as a tree traversal.
Binary Trees and Binary Search Trees
Before talking about how to build a binary tree in JavaScript, there is something we should know.
The child nodes of a parent node are referred to as the left node and the right node.
A binary search tree is a binary tree in which data with lesser values are stored in left nodes while greater ones in right nodes. In another word, the value of the left node should be lesser than the parent node, and then lesser than the right node.
Nodes
function Node(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
this.show = show;
}
function show() {
return this.data;
}
Binary Search Trees
function BST() {
this.root = null;
this.insert = insert;
this.inOrder = inOrder;
this.preOrder = preOrder;
this.postOrder = postOrder;
}
function insert(data) {
var node = new Node(data, null, null);
if (this.root = null) {
this.root = node;
} else {
var current = this.root;
var parent;
for (;;) {
parent = current;
if (data < current.data) {
current = current.left;
if (current === null) {
parent.left = node;
break;
}
} eles {
current = current.right;
if (current === null) {
parent.right = node;
break;
}
}
}
}
}
/**
* to show data in an order:
* left -> parent -> right
*/
function inOrder(node) {
if (node !== null) {
inOrder(node.left);
console.log(node.show() + ' ');
inOrder(node.right);
}
}
/**
* to show data in an order:
* parent -> left -> right
*/
function preOrder(node) {
if (node !== null) {
console.log(node.show() + ' ');
inOrder(node.left);
inOrder(node.right);
}
}
/**
* to show data in an order:
* left -> right -> parent
*/
function postOrder(node) {
if (node !== null) {
inOrder(node.left);
inOrder(node.right);
console.log(node.show() + ' ');
}
}
BST Searches
Searching for the Minimum and Maximum Value
function getMin() {
var current = this.root;
while (current.left !== null) {
current = current.left;
}
return current.data;
}
function getMax() {
var current = this.root;
while (current.right !== null) {
current = current.right;
}
return current.data;
}
Searching for a Specific Value
function find(data) {
var current = this.root;
while(current.data !== data) {
if (data < current.data) {
current = current.left;
} else {
current = current.right;
}
if (current === null) {
return null;
}
}
return current;
}
Removing nodes from a BST
function remove(data) {
this.root = removeNode(this.root, data);
}
function removeNode(node, data) {
if (node === null) {
reurn null;
}
if (data === node.data) {
/** no children */
if (node.left === null && node.right === null) {
return null;
}
if (node.left === null) {
return node.right;
}
if (node.right === null) {
return node.left;
}
/** both the left and the right child are exsisted */
var tmpNode = getSmallest(node.right);
node.data = tmpNode.data;
node.right = removeNode(node.right, tmpNode.data);
return node;
} else if (data < node.data) {
/** search recursively in the left tree */
node.left = removeNode(node.left, data);
return node;
} else {
/** search recursively in the right tree */
node.right = removeNode(node.right, data);
return node;
}
}
function getSmallest(node) {
var current = node;
while (current.left !== null) {
current = current.left;
}
return current;
}
Update a node
update(node, data) {
/** remove the original node */
this.root = this.removeNode(this.root, node.data);
/** insert after removing */
this.insert(data);
}
As the plugin is integrated with a code management system like GitLab or GitHub, you may have to auth with your account before leaving comments around this article.
Notice: This plugin has used Cookie to store your token with an expiration.